Half-Angle Formula and the Area of a Triangle

In triangle $ABC$, Let $a,b,c$ denote the lengths of the sides opposite to the vertices $A,B$ and $C$ respectively. If $a,b,c$ are in arithmetic progression such that $x^2+3x+5=0$ and $3x^2+ax+c=0$ have a common root, then the radius of the smallest circle which touch all the sides of triangle $ABC$ is

Denote Area $\left(∆XYZ\right),P\left(∆XYZ\right)$ and $\left|XY\right|$ by area of the triangle $∆XYZ$, perimeter of the triangle $∆XYZ$ and length of the line segment $XY$ respectively.
Let $ABCD$ be a convex quadrangle and the diagonals $AC$ and $BD$ intersect at $O$. Then

Heron's formula for area of the triangle is $\sqrt{(s+a)(s-a)(s-b)(s-c)}$ 

Heron's formula for area of the triangle is $\sqrt{\left(s\right(s-a\left)\right(s-b\left)\right(s-c)}$ 

Heron's formula for area of triangle is

Write Heron's formula for area of triangle

In a quadrilateral $ABCD,$ it is given that $AB=AD=13, BC=CD=20, BD=24 .$ If $r$ is the radius of the circle inscribed in the quadrilateral, then the integer closest to $r$ is

In a $∆ABC, X$ and $Y$ are points on the segment $AB$ and $AC$ respectively, such that $AX:XB=1:2$ and $AY:YC=2:1$. If the area of $∆AXY$ is $10$ sq. units, then the area of $∆ABC$ in sq. units, is

Let $ABCD$ be a square and $E$ be a point outside $ABCD$ such that $E, A, C$ are collinear in that order. Suppose $EB=ED=\sqrt{130}$ and the areas of triangle $EAB$ and square $ABCD$ are equal. Then the area of square $ABCD$ is :

A triangle with perimeter $7$ has integer side lengths. What is the maximum possible area of such a triangle?

In triangle $ABC, \frac{16\mathrm{Rs}\Delta \sin \frac{A}{2}\sin \frac{B}{2}\cos \frac{C}{2}}{s-c}$ is equal to

If in a triangle $ABC, s(s-a)=(s-b)(s-c)$, then

If $\mathrm{p},\mathrm{ }\mathrm{q},\mathrm{ }\mathrm{r}$ are the lengths of the internal bisectors of angles $\mathrm{A},\mathrm{ }\mathrm{B},\mathrm{ }\mathrm{C}$ of a $\mathrm{\Delta }\mathrm{A}\mathrm{B}\mathrm{C}$ respectively, then $\frac{1}{\mathrm{p}}\cos \frac{\mathrm{A}}{2}+\frac{1}{\mathrm{q}}\cos \frac{\mathrm{B}}{2}+\frac{1}{\mathrm{r}}\cos \frac{\mathrm{C}}{2}$ is equal to ( where a = BC, b = CA, c = AB)

If $p_1, p_2, p_3$ are respectively the length of the perpendicular from the vertices of a $∆ABC$ to the opposite sides, then $p_1{p}_2{p}_3$ is equal to

(where $a=BC, b=AC, c=AB \& R=\text{circumradius of }∆ABC$) 

If in a triangle $a{\cos }^2\left(\frac{C}{2}\right)+c{\cos }^2\left(\frac{A}{2}\right)=\frac{3b}{2},$ then the sides of the triangle are in:

If the length of each side of an equilateral triangle is 10cm, then its area is

If in any triangle, the area of the triangle $∆\le \frac{b^2+c^2}{\lambda },$ then the largest possible numerical value of $\lambda$ is:

The diagonals of a convex quadrilateral intersect in $O.$ What is the smallest area this quadrilateral can have, if the triangles $AOB$ and $COD$ have areas $4$ and $9,$ respectively ?

Find the area of a triangle having two sides of lengths $90 \mathrm{m}$ and $65 \mathrm{m}$ and an included angle of $105°$. [Enter the value correct up to three significant figures excluding units]

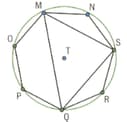
A garden is shaped in the form of a regular heptagon (seven-sided), $MNSRQPO$. A circle with centre $T$ and radius $25 \mathrm{m}$ circumscribes the heptagon as shown in the diagram below. The area of $△MSQ$ is left for a children's playground, and the rest of the garden is planted with flowers. Find the area of the garden planted with flowers. [Enter the value correct up to three significant figures excluding units]